Three rival gangs face-off. Someone fires a shot. Bullets fly. People die. Such typical scenes in a John Woo film illustrate the concept of stochastic battles. Lanchester first developed useful mathematic models of such conflicts during WWI, when machine guns changed the nature of warfare.

The US Navy developed Lanchester’s ideas further when executing its island-hopping strategy during WWII. As you might imagine, Japan studied Lanchester Theorems in earnest after the war and adapted them to commercial battles for market dominance. Several manga-style tutorials on Lanchester strategy were published in Japan and the ones I have from Shinichi Yano became corner stones of my analytic library many decades ago. It has been more than five years since I published such analysis for the AMLCD industry, so here is an update.
Machine guns spraying bullets is an apt analogy for stochastic conflict. Unlike one-to-one samurai duels, in which a skilled swordsman may lose to three attackers, the spray of bullets on a modern battlefield means a smaller advantage is needed for victory. Turning Lanchester’s Square Law into a heuristic (rule of thumb) reveals that a force having a 70% advantage (a factor of 2^[3/4] actually) may prevail over rivals. Put another way, any rival having 60% of the leader’s fighting power is within shooting range of being a new leader.
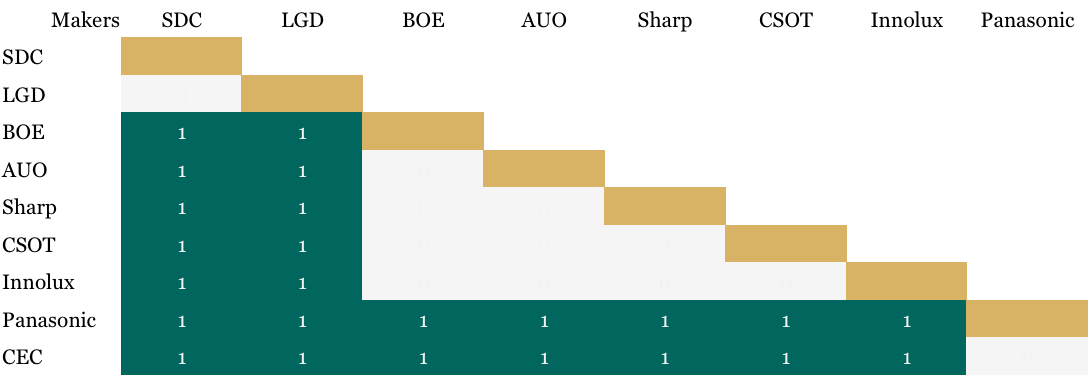
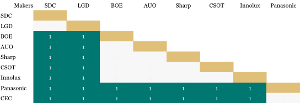
If we apply this principle to large-substrate (Gen-7 and larger glass) capacity battles, we see that Samsung Display (SDC) and LG Display (LGD) might win any wild gunfight. No rivals are within shooting range if we use 2015 area capacity as a proxy for firepower. In the diagram, green blocks under the LGD column indicate dominated rivals. In contrast, Beijing Oriental Electronics (BOE) is within shooting range of four smaller rivals. I anticipate that BOE will add a lot of firepower later this decade, however. If BOE adds 43% of capacity relative to LGD, then LGD comes into shooting range. What a great summer movie that would make!
Market structure is another application of Lanchester’s theorems we can apply here. The smallest share of fighting power required to stabilize a market is about 26% ([1/[1+2^[3/2]]] actually). Both SDC and LGD have the required shares this year, so we should expect more stability in the large-panel market than in prior decades. Similarly, Innolux (including Foxconn) has a stabilizing share (29%) of Gen-6 and smaller glass capacity. Rivalry is increasing, however, and most small panel gangs are within shooting distance of each other. The key observation here is that no producer is close to the 42% capacity share required for market leadership.
The AMLCD industry remains a panopoly. There is no leader. When all capacity is considered, even SDC and LGD each have less than a 22% share. Declining shares in Taiwan and Japan will offset rising capacity shares in China. Thus, rivalry will increase and most producers will be within shooting range of their rivals for the rest of this decade.
Zapf that Panel
But wait! There’s more! An old analyst can’t sign off without updating his Zapf-Mandelbrot distribution model for large panels. For those unaware of such esoterica, Zapf was the guy who noticed that the frequency of English word use followed a power curve. A common word such as “the” was used much more frequently than “blateration” (i.e. this blog). The roll-off is quite predictable for various kinds of documents.
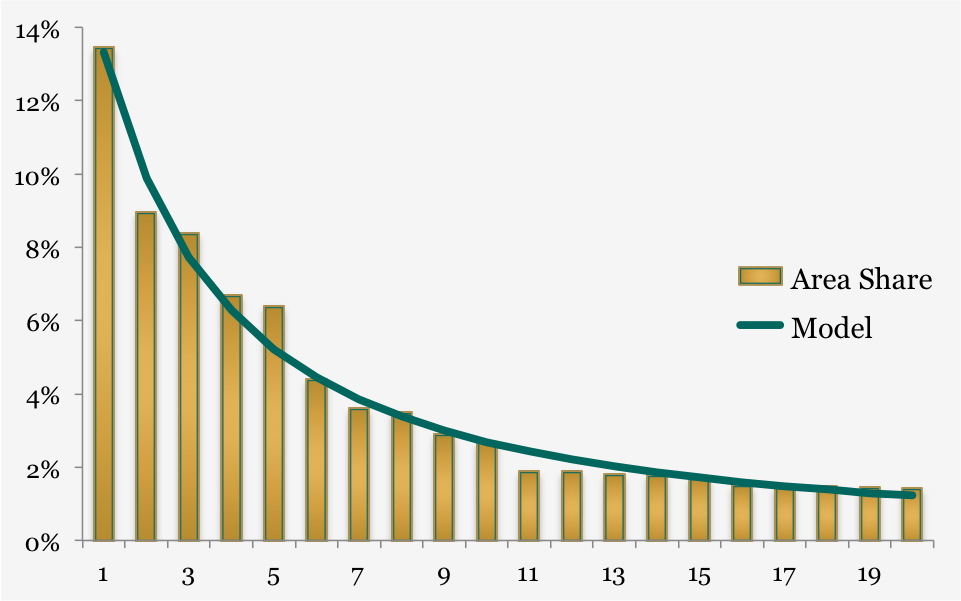
If we examine the display area shipped by large-panel type last year, we see a classic power curve. Mandelbrot (who pioneered many aspects of chaos and fractals) created a more general expression of Zapf’s ideas that I model here as [N + 3.2]^-1.4 where N is the rank position of each panel type by area share. For those interested in the data, the top three panel types were 32” HD, 40” FHD and 42” FHD. There were 149 other panel types shipped in 2014 but I plot only the top 20 here. The implication is that the AMLCD industry still exhibits some classic behavior after many years of alleged innovation or change. There is nothing mysterious about the distribution of panel types: they fall along a power curve just as the frequency of English words do. Thanks for reading my blateration, which used blateration three times and will forever skew the data! – David Barnes